Finding an upper bound

The puzzle asks us to maximise the probability of drawing a red ball, given that we choose a bucket at random. This can be expressed as

\[p(red) = 0.5p_1 + 0.5p_2.\]

This also makes sense, right? If we choose a bucket at random, we have a 50-50 chance of selecting either bucket \(A\) or \(B\). The probability of selecting urn \(A\) is 50%, and the probability of drawing a red ball from urn \(A\) is given by \(p_1\). Likewise, the probability of selecting urn \(B\) is 50%, and the probability of selecting a red ball from urn \(B\) is given by \(p_2\). Our job is now to maximise \(p(red)\).

First, consider urn \(A\). Which combination \((x_1, y_1)\) maximises \(p_1\)? Well, it seems obvious that if we set \(y_1 = 0\), then there are noe blue balls in urn \(A\). Consequently, all the balls in this urn will be red. In other words, any value of \(x_1\) will yield \(p_1 = 1\). In fact, setting \(y_1 = 0\) is the only way to get \(p_1 = 1\). Too see this, fix \(x_1\) at any value between 1 and 50 (because there always has to be at least one ball in the urn) and try adjusting \(y_1\).

Setting \(y_1 = 0\) seems like a good place to start. Again, remember that \(x_1 \in [1, 50]\). There has to be at least one ball and at most 50 in urn \(A\).

Now consider urn \(B\). If there are more red balls in urn \(A\) than in urn \(B\), then \(x_2 < y_2\). In plain english, there will be more blue balls than red balls in urn \(B\). Another way of writing this is \(x_2 + 1 \leq y_2\). This reformulation is important because it gives us an expression for the upper bound of \(p_2\), the maximum value it can take. The upper bound is obtained by substituting the inequality into our expression for \(p_2\),

\[p_2 = \dfrac{x_2}{x_2 + y_2} \leq \dfrac{x_2}{x_2 + x_2 + 1} = \dfrac{x_2}{2x_2 + 1}.\]

Locating the maximum

What else do we know about \(x_2\)? Well, since we have 50 red balls, we know that the number of red balls in urn \(B\) is the total number of red balls minus the number of red balls in urn \(A\),

\[x_2 = 50 - x_1, \text{ where } x_1 \in [1, 50].\]

Again, substituting this into \(p_2\) yields

\[p_2 \leq \dfrac{50-x_1}{2(50 - x_1) + 1} = \dfrac{50-x_1}{101 - 2 x_1}.\]

This tells us that the upper bound of \(p_2\) is given by \((50 - x_1) / (101 - 2x_1)\).

Since \(p_1\) is always 1 when \(y_1 = 0\), our main concern is to find the value of \(x_1\) that maximises \(p_2\). We can plot these probabilities with the following code:

import matplotlib.pyplot as plt
import numpy as np

def p2_max(x1):
    """Probability of drawing a red ball from urn B given number of balls in urn A."""
    return (50 - x1) / (101 - 2*x1)

# Number of balls in urn A 
x1 = np.arange(1, 51)

# Plotting probabilities
plt.figure(figsize=(10, 6))

with plt.style.context("fivethirtyeight"):
    plt.plot(x1, p2_max(x1))
    plt.xlabel("number of red balls in urn A")
    plt.ylabel(r"$\tilde{p}_2$")
    plt.title(r"Upper limit of $p_2$")
    plt.show()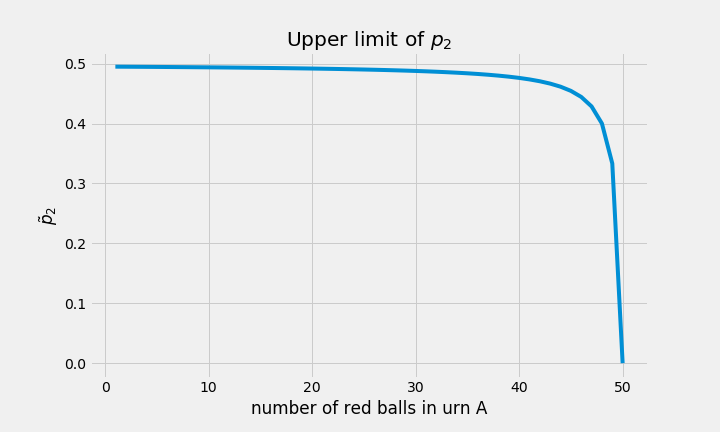

From the figure, it seems that \(p_2\) is maximised when \(x_1 = 1\). We can confirm this by analysing the derivative of the upper bound of \(p_2\) (denoted \(\tilde{p}_2\)) with respect to \(x_1\),

\[\dfrac{d\tilde{p}_2}{d x_1} = \dfrac{d}{dx_1} \Bigg(\dfrac{50-x_1}{101 - 2 x_1}\Bigg) = \dfrac{-1}{(101 - 2 x_1)^2}.\]

Note that \(d\tilde{p}_2/d x_1 < 0\) for all \(x_1 \in [1, 50]\). Since the derivative is always negative, \(\tilde{p}_2\) is monotonically decreasing when \(x_1 \in [1, 50]\). And since \(\tilde{p}_2\) is the largest value \(p_2\) can take, the probability of drawing a red ball given that you choose urn \(B\) is indeed maximised when \(x_1 = 1\). Strictly speaking, we could reach the same conclusion without reparameterising \(p_2\) in terms of \(x_1\), but I find this approach slightly more intuitive.

Putting it all together

To calculate the probability of drawing a red ball when selecting an urn at random, we simply plug in \(x_1 = 1\) and \(x_2 = 50 - x_1 = 50 - 1 = 49\) into our expression for \(p(red)\):

\[p(red) = 0.5\dfrac{1}{1} + 0.5\dfrac{49}{99} = 0.7474.\]

In other words, to maximise the probability of drawing a red ball when an urn is chosen at random, one of the urns should contain a single red ball, and the other should contain the rest.

There are probably many ways to implement a pure Python solution to this problem. One approach is the following:

import itertools as it

def p(num_red, num_blue, urn_prob=0.5, total_balls=100, red_balls=50):
    """Calculate probability of drawing a red ball after selecting an urn at random."""
    p1 = num_red / (num_red + num_blue)
    p2 = (red_balls - num_red) / (total_balls - num_red - num_blue)
    return urn_prob*p1 + (1 - urn_prob)*p2

def print_results(results):
    """Calculate and print results of maximising p(red)"""
    max_prob = max(results.values())
    num_red, num_blue = max(results, key=results.get)
    print(f"Probability of selecting red ball: {max_prob}")
    print(f"One of the urns must contain {num_red} red balls and {num_blue} blue balls.")

# Find find number of balls that maximise probability of drawing a red from a random urn
x1 = y1 = range(1, 51)
balls = it.product(x1, y1)
results = {
    (red, blue): p(red, blue) 
    for red, blue in balls 
    if (red + blue) != 100
}

# Probability of selecting red ball: 0.7474747474747475
# One of the urns must contain 49 red balls and 50 blue balls.
print_results(results)

For extra credit, we can find the combination of colours that maximise the probability of drawing a red ball from a random urn when the when we have 25 and 200 of each colour, respectively:

# 25 of each colour
N = 25
x1 = y1 = range(1, N + 1)
balls = it.product(x1, y1)

twentyfive = {
    (red, blue): p(red, blue, red_balls=N, total_balls=2*N) 
    for red, blue in balls 
    if (red + blue) != 2*N
}

# Probability of selecting red ball: 0.7448979591836735
# One of the urns must contain 24 red and 25 blue.
print_results(twentyfive)

# ---------------------------------------------------------

# 200 of each colour
N = 200
x1 = y1 = range(1, N + 1)
balls = it.product(x1, y1)

twohundred = {
    (red, blue): p(red, blue, red_balls=N, total_balls=2*N) 
    for red, blue in balls 
    if (red + blue) != 2*N
}

# Probability of selecting red ball: 0.7493734335839599
# One of the urns must contain 199 red and 200 blue.
print_results(twohundred)

Bonus: Varying the number of balls and buckets probabilities

Just for fun, let’s plot two more functions:

1. \(p(red)\) as a function of the number of balls \(N\).
2. \(p(red)\) as a function of the the probability \(\alpha\) of selecting a bucket.

def get_probs(n=100, alpha=0.5, **kwargs):
    """Return probability of drawing a red ball when selecting bucket at random."""
    x1 = y1 = range(1, n + 1)
    balls = it.product(x1, y1)

    results = {
        (red, blue): p(red, blue, urn_prob=alpha, **kwargs) 
        for red, blue in balls 
        if (red + blue) != 2*n
    }

    return max(results.values())

# Fixing bucket probability alpha = 0.5 and varying N
max_probs = []
N = [i for i in range(2, 501)]

# Calculating probabilities
for n in N:
    max_probs.append(get_probs(n=n, total_balls=2*n, red_balls=n))
    
# Plotting
plt.figure(figsize=(10, 6))

with plt.style.context("fivethirtyeight"):
    plt.plot(N, max_probs)
    plt.xlabel("$N$")
    plt.ylabel("$p(red)$")
    plt.title("Probability of drawing a red ball")
    plt.show()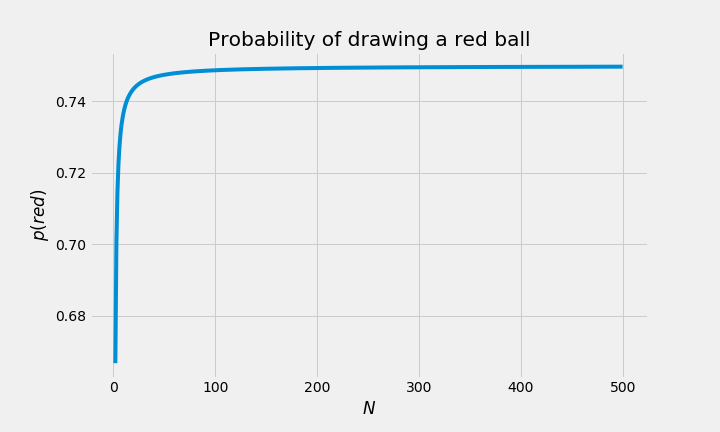

# Fixing number of coloured balls N = 100 and varying alpha
max_probs = []
N = 100
alpha = np.arange(0, 1.01, step=0.01)

# Calculating probabilities
for a in alpha:
    max_probs.append(get_probs(alpha=a, total_balls=2*N, red_balls=N))
    
# Plotting
plt.figure(figsize=(10, 6))

with plt.style.context("fivethirtyeight"):
    plt.plot(alpha, max_probs)
    plt.xlabel(r"$\alpha$")
    plt.ylabel("$p(red)$")
    plt.title("Probability of drawing a red ball")
    plt.show()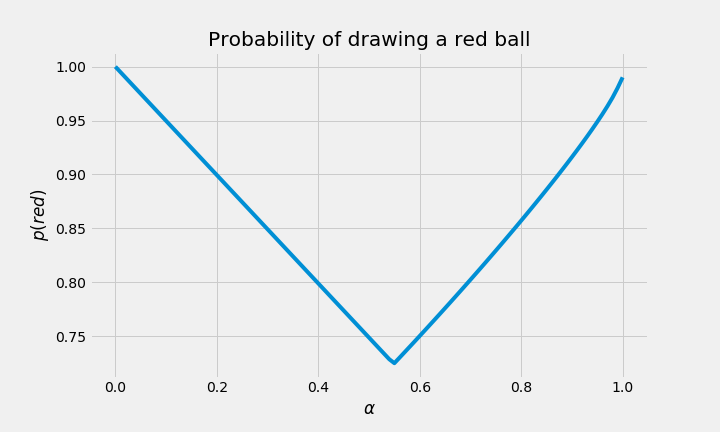

That’s it, hope you enjoyed it as much as I did!