Last week’s Riddler classic posed the following problem:
“You’ve won two gift cards, each loaded with 50 free drinks from your favorite coffee shop, Riddler Caffei-Nation. The cards look identical, and because you’re not one for record-keeping, you randomly pick one of the cards to pay with each time you get a drink. One day, the clerk tells you that he can’t accept the card you presented to him because it doesn’t have any drink credits left on it. What is the probability that the other card still has free drinks on it? How many free drinks can you expect are still available?”
Original solution
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
# List to keep track of credit on the other card
other_card = []
runs = 0
while runs < 500000:
# Initial setup, two cards worth 50 free coffees each
cards = {0: 50, 1: 50}
done = False
while not done:
# Pick a card at random
pick_card = stats.bernoulli.rvs(p=.5)
if cards[pick_card] == 0:
# If there is no credit left, check credit of other card and restart
other_card.append(cards[1 - pick_card])
runs += 1
done = True
else:
# If there is credit left, subtract one coffee
cards[pick_card] -= 1
# Plot results
other = np.array(other_card)
plt.figure(figsize=(10, 6))
sns.distplot(other)
plt.title("Distribution of credit on other card", size=18)
plt.show()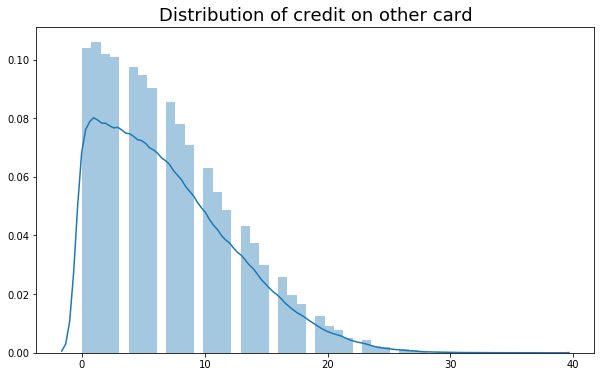
# Probability that other card has free coffee left:
print(1 - np.where(other == 0, True, False).mean())
# 0.9204
# Expected number of free coffees left on other card:
print(np.mean(other))
# 7.043334Other approaches
Again, a very elegant answer can be found at Jason Ash’s blog. He also offers a clever analytical solution to the problem. The following code is a slightly modified version Jason’s implementation:
from random import randint
# List to keep track of credit on the other card
other_card = []
num_iters = 10**5
for i in range(num_iters):
# Initial setup, two cards worth 50 free coffees each
cards = [50, 50]
# Pick a card at random, use until refused service
while min(cards) > -1:
pick_card = randint(0, 1)
cards[pick_card] -= 1
# Save remaining credit on other card
other_card.append(max(cards))
remaining_credit = np.array(other_card)
# Probability that other card has free coffee left:
print(1 - np.where(remaining_credit == 0, True, False).mean())
# 0.92015
# Expected number of free coffees left on other card:
print(np.mean(remaining_credit))
# 7.01295Reading Jason’s solutions is really inspiring, both in terms of how he attacks the problems and how efficiently he implements simulations. Please check out his site for more good stuff!