Original solution

Spelling bees aren’t really a thing where I’m from, so in the first iteration of my solution I made the assumption that a round ends when a contestant gets a word wrong. The next round then starts with the player immediately following the recently eliminated contestant. This led to some experimentation with ordered dictionaries and reshuffling lists. I also wanted to get a distribution of the estimated win rate for the best player, so I ran the multiple simulations.

def spelling_bee_winners(players, best_player_starts=True, num_bees=10**3, to_percent=False):
    ''' Simulate spelling bees and return distribution of victories.'''
    
    results = {name: 0 for name in players}

    # Simulate spelling bee
    for i in range(num_bees):

        names = players.copy()
        probs = [.9 + 0.01*i for i in range(10)]
        
        if best_player_starts:
            probs = probs[::-1]
        else:
            names = names[::-1]

        spelling_bee = OrderedDict([(name, prob) for name, prob in zip(names, probs)])

        # This is a round, restarts when player gets eliminated
        while len(spelling_bee) > 1:

            for player, prob in spelling_bee.items():

                # Sample a word from the dictionary
                word = np.random.uniform(size=1)

                # If player doesn't know word, remove from competition, reorder contestants and start new round
                if word > prob:
                    remove = names.index(player)

                    del names[remove]
                    del probs[remove]
                    
                    # Check if eliminated player is the last player
                    if len(names) - remove == 1:
                        spelling_bee = OrderedDict([(name, prob) for name, prob in zip(names, probs)])
                        break
                    else:
                        new_players = names[remove:] + names[:remove]
                        new_probs = probs[remove:] + probs[:remove]
                        spelling_bee = OrderedDict([(name, prob) for name, prob in zip(new_players, new_probs)])
                        break
        
        # Record victory for winning player
        for player in spelling_bee.keys():
            results[player] += 1
        
    # Convert score to percent
    if to_percent:
        for player in results.keys():
            results[player] = results[player] * (1 / num_bees)
    
    return results


def simulations(players, num_bees=10**3, simulations=100, best_player_starts=True, to_percent=False):
    ''' Simulate spelling bees to get average and std. deviations. '''
    results = np.zeros(simulations)
    
    for i in range(simulations):
        best_first = spelling_bee_winners(players, best_player_starts=best_player_starts, num_bees=num_bees, to_percent=to_percent)
        results[i] = best_first['A']

    return results


def plot_results(results, bins=20, label=None):
    ''' Helper function to plot results of simulations.'''
    average = round(np.mean(results), 4)
    plt.hist(results, bins=bins, alpha=0.7, label=f'{label} (avg.: {average})')
    plt.axvline(average, linestyle="--", color='k')
    
    
# Simulating spelling bees
players = ["A", "B", "C", "D", "E", "F", "G", "H", "I", "J"]
best_first = simulations(players, best_player_starts=True, to_percent=True)
best_last = simulations(players, best_player_starts=False, to_percent=True)

# Plotting comparisons
plt.figure(figsize=(8, 6))
plot_results(best_first, label='First player')
plot_results(best_last, label='Last player')
plt.title('Starting first vs. starting last', size=20)
plt.legend()
plt.show()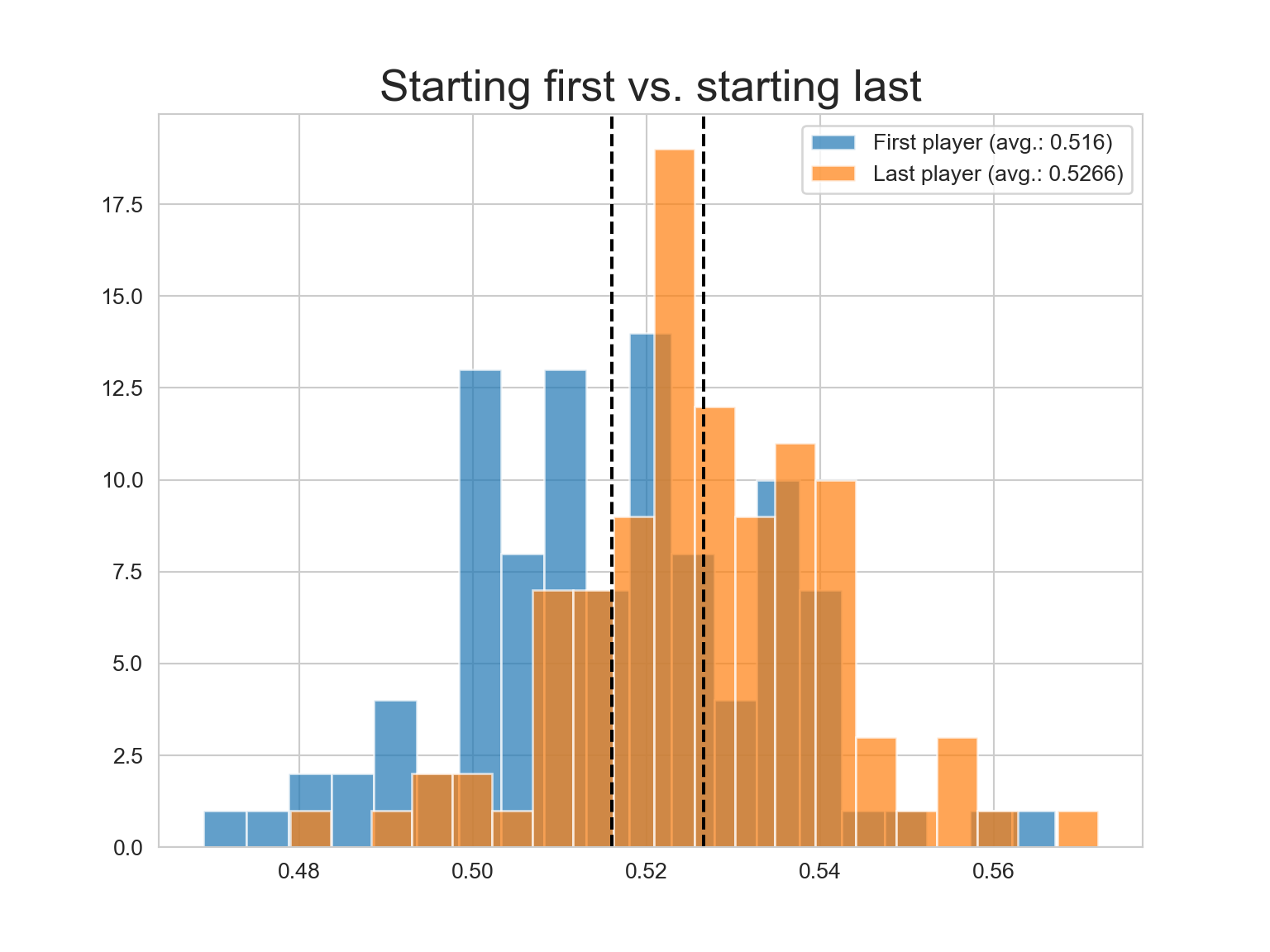

So it turns out the the order of the contestants doesn’t really matter that much. The most knowledgable player slightly increases her probability of winning if she goes last.

Revised solution

As it turns out, I think I overcomplicated the rules of elimination somewhat due to the fact that I don’t really know how a spelling bee works. I quite like this approach by Josh Nees, so I decided to write my own variant of it. His is a cleaner implementation than my original proposal, the only thing I added was the potential outcome where all players get a word wrong and the game ends in a tie.

def spelling_bee_winners(players, best_player_starts=True, num_bees=10**3, to_percent=False):
    ''' Simulate spelling bees and return distribution of victories.'''

    results = {name: 0 for name in players}
    ties = 0

    # Simulate spelling bee
    for i in range(num_bees):
        
        contestants = players.copy()
        
        if best_player_starts:
            contestants = contestants[::-1]

        # This is a round, restarts when player gets eliminated
        while len(contestants) > 1:
            
            for contestant in contestants:
                
                # Sample a word from the dictionary
                word = np.random.randint(0, 101, size=1)

                # If player doesn't know word, remove from competition, reorder contestants and start new round
                if word > contestant:
                    contestants.remove(contestant)
            
        # If all contestants fail, the round ends in a tie
        if len(contestants) == 0:
            ties += 1
        # Record victory for winning player
        else:
            results[contestants[0]] += 1
        
    # Convert score to percent
    if to_percent:
        results = {player: (score / num_bees) for player, score in results.items()}
    
    return results, ties
    
    
# Simulating spelling bees
players = [i for i in range(90, 100)]
num_bees = 500000

best_first, _ = spelling_bee_winners(players, best_player_starts=True, num_bees=num_bees, to_percent=True)
# Probability of winning: 0.512562

best_last, _ = spelling_bee_winners(players, best_player_starts=False,  num_bees=num_bees, to_percent=True)
# Probability of winning: 0.519574